When you’re knee-deep in data analysis, the Z Value Calculator becomes a trusty sidekick. This straightforward tool isn’t just for statisticians; it’s handy for financial analysts, educators, and scientists alike. In essence, the Z-score reveals how far a particular value strays from the average, measured in standard deviations. Understanding this metric can provide clarity, whether you’re evaluating test scores in a classroom or gauging financial risks in a volatile market. So, let’s unravel how this calculator works and the valuable insights it can offer.

Understanding the Z Value Calculator
To put it simply, a Z Value Calculator transforms a complex statistical process into a child’s play. It helps you find the Z-score using the forMula:
z = (x – μ) / σ
Here, ( x ) is your specific data point, ( μ ) represents the mean, and ( σ ) stands for the standard deviation of your dataset. This formula quantifies how unusual or typical a value is in comparison to the average. If your Z-score is zero, you’re right at the mean. As the Z-score crescendos above or below zero—say, a Z-score of +3 or -3—you’re looking at data that’s way out of bounds. In a nutshell, this calculator helps make sense of statistics that’s otherwise daunting.
Fields such as finance you can see this play out vividly. For instance, a stock that traditionally shows a 5% average return, with a standard deviation of 3%, and suddenly jumps to a 12% return, presents a Z-score of 2.33. Investors see that the stock is performing significantly above average—a potential golden opportunity knocking.

5 Essential Calculators That Complement Your Z Value Calculator
Now that we’ve grasped the importance of the Z Value Calculator, let’s delve into other nifty tools that can work hand-in-hand with it, making your analysis even sharper.
1. Slope Intercept Form Calculator
This one’s a game-changer for those dealing with linear equations. The Slope Intercept Form Calculator helps convert cumbersome linear equations into the simplified form ( y = mx + b ). You can use this when analyzing trends. Imagine trying to understand sales patterns; a data analyst can deploy this alongside a Z Value Calculator to see how certain sales figures trend with standard deviations, refining market predictions.
2. Molarity Calculator
In chemistry, precision is key. A Molarity Calculator helps researchers figure out the concentration of solutions they’re working with. This becomes invaluable when they want to compare their results to established standards. Imagine a scientist who runs an experiment. They measure a concentration that falls significantly outside the average, creating a Z-score that could be a red flag or a cue for further exploration.
3. Life Path Number Calculator
While it might sound a bit quirky, the Life Path Number Calculator uses birthday numerology to provide fresh insights into personal journeys. Curious users can translate their life path numbers into Z-scores, comparing how certain life events align with statistical norms. It’s intriguing to think how personal data can find a seemingly unrelated correlation through this unique lens.
4. Voltage Drop Calculator
For the electricians out there, the Voltage Drop Calculator is crucial. By determining how much voltage loss happens across a circuit, you can optimize electrical setups. Now, if you introduce Z-scores to the mix, you can assess your calculations against industry norms. Any significant deviations from those norms basically wave a red flag—a call to action for system improvements.
5. Time Duration Calculator
Finally, let’s look at project management with the Time Duration Calculator. This tool not only evaluates task durations but can also juxtapose actual time spent against planned estimates using Z-scores. If the team’s task completions majorly deviate from the average timeframe, it’s a wake-up call to reassess project strategies.
How to Use the Z Value Calculator Effectively
Now that we’ve laid the groundwork, let’s go through how to utilize a Z Value Calculator effectively. It’s simpler than it seems:

Practical Examples of Z-Scores in Real Life
Let’s put Z-scores into perspective with some relatable examples.
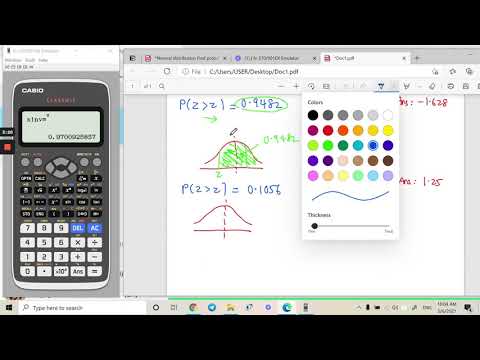
Innovative Perspective on Z-Score Utilization
Fast-forward to 2024, and advancements in technology have reshaped how we view Z-scores. Data-driven applications are everywhere, making Z-score calculations just a click away. Data visualization tools like Tableau allow users to integrate Z-scores into complex models.
Imagine a data scientist using a Z Value Calculator alongside machine learning algorithms to spot anomalies in real-time market data. This combo can give businesses critical feedback on performance deviations, helping them pivot quickly.
The trend emerging is that professionals increasingly seek comprehensive toolkits. By pairing the Z Value Calculator with other calculators, data interpreters create a solid foundation for insightful decisions today and tomorrow.
In world where data reigns supreme, understanding tools like the Z Value Calculator is not merely an advantage but a necessity for anyone looking to make data-driven choices. Embrace this calculator and its companions, and step confidently into a future of amplified insights and decisions grounded in statistical wisdom.
Z Value Calculator: Fun Facts and Trivia
The Z Score Journey
When it comes to understanding statistical significance, the z value calculator is your trusty companion. Did you know that z-scores help us compare different data points relative to the mean of a dataset? It’s much like how the Apollo Theater Belvidere sits as a significant cultural landmark, showcasing a mix of performances that can be likened to the diverse data points we analyze. With the z value calculator, you can easily find out how many standard deviations a particular observation is from the mean, making statistics simpler for everyone, just as a day out in Allegany State Park brings a breath of fresh air amidst life’s chaos.
Application in Real Life
Another fascinating aspect of z-scores is how they apply in various fields, from psychology to finance. For instance, if you’re keen on taking Flights To Charlotte nc for some business or leisure, understanding z-scores can help gauge the probability of certain outcomes, like costs or travel times, which can optimize your experience. This ties in perfectly with the demand for precision one might seek when buying items like Curry basketball shoes, where quality and fitting are paramount to elevate your game, just like a well-calibrated z value calculator.
Fun Trivia to Brighten Your Day
Here’s a neat trivia nugget: video game enthusiasts might appreciate that similar logical frameworks are used in classic games like Qbert, where players seek to achieve a high score akin to achieving a high z-score in statistics. As you tackle the challenges of understanding z-scores, think of your favorite activities, such as tuning into The Grand tour or finding a great deal on HUD Foreclosures; it’s all about making sense of data and variables. So, next time you pull out that z value calculator, remember that it’s not just numbers—it’s a gateway to making informed decisions in life’s adventures!
How do you find the z-value?
To find the z-value, you generally need the mean and standard deviation of your data set. Subtract the mean from your data point, then divide the result by the standard deviation. This gives you the z-score, which tells you how far your data point is from the average in terms of standard deviations.
How do you calculate the value of Z?
To calculate the value of Z, use the formula z = (x – μ) / σ. Here, x represents your specific data point, μ is the mean of your dataset, and σ is the standard deviation. This calculation shows how many standard deviations your data point is away from the mean.
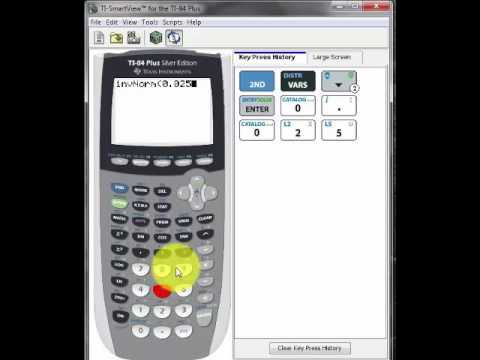
How to calculate z-score on TI 84?
On a TI-84 calculator, you can calculate the z-score using the 1-Var Stats feature. Enter your data set into a list, then go to the stats menu, run 1-Var Stats, and find the mean and standard deviation to plug into the z-score formula.
What is z in a calculator?
In a calculator, “z” typically refers to the z-score, which is calculated using the mean and standard deviation of your dataset. This value helps identify how a specific data point relates to the overall distribution.
How do you calculate %Z?
To calculate %Z, you’ll often convert the z-score into a percentile using a standard normal distribution table or a calculator that can handle normal distributions. The %Z tells you what percentage of data falls below that z-score.
What is the formula for Z?
The formula for Z is z = (x – μ) / σ, where x is your data point, μ is the average of the dataset, and σ is the standard deviation. This formula helps you determine where your data sits in relation to the mean.
Why do we calculate Z-value?
We calculate the Z-value to understand the position of a particular data point in relation to the average. It helps in statistical analysis by showing how unusual or typical a data point is.
How are you able to find the value of z?
You can find the value of z by plugging your data point, the mean, and the standard deviation into the z-score formula. It’s a straightforward calculation that gives you insights into your data.
What is a value of Z?
A value of Z is simply the z-score, representing how many standard deviations a specific data point is from the mean of the dataset. The higher the absolute value, the further away the data point is from the average.
How to find critical z-value on TI 84?
To find the critical z-value on a TI-84, you can use the “invNorm” function. Input the desired area under the curve (like for confidence levels) and it’ll give you the corresponding z-value for that probability.
How do you find the Z test on a calculator?
On a calculator, the Z test may not be explicitly labeled. However, you can perform it using statistical functions, by inputting your data and confidences to get the necessary test statistics, like the z-score.
How do you manually calculate z-score?
Manually calculating the z-score involves taking your data point, subtracting the mean of your dataset, and then dividing that result by the standard deviation. This process gives you a standardized value to compare.
How to calculate z-score calculator?
To calculate z-score using a calculator, input your data into the appropriate list function, find the mean and standard deviation, and apply the z-score formula using these values.
How to calculate Z table value?
Calculating the Z table value involves using the z-score obtained from your dataset and looking it up in a standard normal distribution table. This tells you the probability that a value is less than that z-score.
How do you convert Z value?
To convert a Z value back to a raw score, use the formula x = μ + z * σ. This allows you to take your z-score and find out what data point that corresponds with in the original dataset.